Files CCore/inc/Tree.h CCore/src/Tree.cpp
Subfolders CCore/inc/tree CCore/src/tree
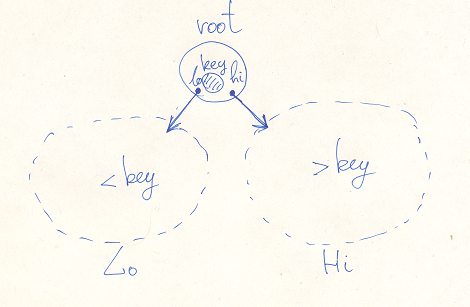
Binary trees is an important class of data structures. A tree consists of a set of elements, each element has a unique key. Keys are comparable and form a linear ordered set. A non-empty tree has a root element and two subtrees: Lo and Hi. Elements in the Lo subtree have a lower keys than the root element. The same way, elements in the Hi subtree have a higher keys than the root element.
Tree operation complexities are O(tree height). To be efficient, a tree must have a limited height. To achieve this there are different methods. We use two most important of them: Radix Tree and Red-Black Tree. The first is applicable to the key types with the limited value range, like integral types.
The height of the Radix Tree is limited by the log(value range volume).
Red-Black Tree has a colored arrows. Each arrow is either red or black. Some properties must be satisfied: there is no two consecutive red arrows, all tree leaves have the same black height. The height of the Red-Black Tree is limited by the 2*log(number of elements). So for these trees operations has a practically constant time limit.
Trees are useful for building maps.
CCore provides a variety of intrusive trees, the same way as a lists. They are available through the header CCore/inc/Tree.h.
CCore has four kind of tree links, each with a tree algorithms sets. To define a tree node you must include one of this links in the class:
struct Node
{
TreeLink<Node,unsigned> link;
....
};
Then use one of Algorithm Packages to operate on trees:
using Algo = TreeLink<Node,unsigned>::RadixAlgo<&Node::link> ;
The TreeLink is a simplest tree link. It has three members: pointers to the Lo and Hi subtrees and the key. The key is unique across all tree.
template <class T,class K>
struct TreeLink
{
T *lo;
T *hi;
K key; // unique
using Node = TreeLink<T,K> ;
template <TreeLink<T,K> T::* LinkMember,class KRef=K> struct BinAlgo;
template <TreeLink<T,K> T::* LinkMember> struct RadixAlgo;
};
There are two Algorithm Packages: BinAlgo with basic binary tree operations and RadixTree, which extends BinAlgo with radix tree operations. The first package has the additional template parameter: KRef. If the K is a lightweight type, then use the default KRef equals K. But for more complicated types, you may use const K & instead or even a completely different type. This type is used to pass key arguments. RadixTree requires the K to be an unsigned integral type.
struct BinAlgo
{
// node!=0
// root_ptr!=0
static Node & Link(T *node) { return node->*LinkMember; }
Link() extracts link from the object.
// Find static T * Find(T *root,KRef key); // == key static T * FindMin(T *root); static T * FindMin(T *root,KRef key); // min >= key static T * FindMax(T *root); static T * FindMax(T *root,KRef key); // max <= key
Find...() is a family of searching functions. The first argument is a tree root pointer. It may also be a subtree root. The second argument (if any) is a key value. Keys must be 3-Way comparable using the function Cmp(KRef,K). Each function returns a pointer to the found element, or null if the required element does not exist.
Find() is searching for the element with the given key.
FindMin() is searching for the element with the minimum key in the tree.
FindMin(,key) is searching for the element with the minimum key in the tree, greater or equal than the given key.
FindMax() is searching for the element with the maximum key in the tree.
FindMax(,key) is searching for the element with the maximum key in the tree, less or equal than the given key.
// Locate static T ** Locate(T **root_ptr,KRef key); static T ** LocateMin(T **root_ptr); static T ** LocateMin(T **root_ptr,KRef key); // min >= key static T ** LocateMax(T **root_ptr); static T ** LocateMax(T **root_ptr,KRef key); // max <= key
Locate...() is another family of searching functions. It does the same as the correspondent Find...() function, but gets another input. It takes not the root pointer, but a non-null pointer to the root pointer variable. The return value is another double pointer: it is the original root_ptr or the pointer to the element pointer in the parent element. It is null, if the element is not found.
These functions are required by the Del...() implementation, you probably wouldn't use them.
// Del static T * DelRoot(T **root_ptr); // (*root_ptr)!=0 static T * Del(T **root_ptr,KRef key); static T * DelMin(T **root_ptr); static T * DelMin(T **root_ptr,KRef key); static T * DelMax(T **root_ptr); static T * DelMax(T **root_ptr,KRef key); static void Del(T **root_ptr,T *node); // node!=0 template <class TestFunc,class DelFunc> static void DelIf(T **root_ptr,TestFunc test_func,DelFunc del_func); // root_ptr!=0
Del...() deletes the element from the tree and returns the pointer to this element (or null, if the element is not found). The first argument is a (non-null) root double pointer, this variable will be updated as the root is changed during the operation.
DelRoot() deletes the root element. The element must exist.
Del(root_ptr,node) deletes the given element form the tree. node must not be null.
The remaining Del...() functions search the element like the Find...() do and delete it.
DelIf() performs the massive delete operation. The first argument is a (non-null) root double point. The second argument is a functor. This functor checks the tree node and determines if it should be deleted. The signature of this functor is boolable (T *node). If it returns true, the node will be deleted. The third argument is a delete functor. It has the signature void (T *node) and is called to delete the node.
// struct NodePtr
struct NodePtr
{
T **node_ptr;
NodePtr(T **node_ptr_) : node_ptr(node_ptr_) {}
T ** operator + () const { return node_ptr; }
bool operator ! () const { return !node_ptr; }
T * node() const { return *node_ptr; }
};
NodePtr wraps a double pointer to an element. It is used by Root methods to return locate...() results.
// struct Root
struct Root
{
T *root;
// constructors
Root() { init(); }
// methods
void init() { root=0; }
T * operator + () const { return root; }
bool operator ! () const { return !root; }
// find
T * find(KRef key) const { return Find(root,key); }
T * findMin() const { return FindMin(root); }
T * findMin(KRef key) const { return FindMin(root,key); }
T * findMax() const { return FindMax(root); }
T * findMax(KRef key) const { return FindMax(root,key); }
// locate
NodePtr locate(KRef key) { return Locate(&root,key); }
NodePtr locateMin() { return LocateMin(&root); }
NodePtr locateMin(KRef key) { return LocateMin(&root,key); }
NodePtr locateMax() { return LocateMax(&root); }
NodePtr locateMax(KRef key) { return LocateMax(&root,key); }
// del
T * del(KRef key) { return Del(&root,key); }
T * delMin() { return DelMin(&root); }
T * delMin(KRef key) { return DelMin(&root,key); }
T * delMax() { return DelMax(&root); }
T * delMax(KRef key) { return DelMax(&root,key); }
void del(T *node) { Del(&root,node); }
template <class TestFunc,class DelFunc>
void delIf(TestFunc test_func,DelFunc del_func) { DelIf(&root,test_func,del_func); }
};
};
Root encapsulates a root pointer and tree operations. Its methods are direct calls of the correspondent functions.
struct RadixAlgo : BinAlgo { // Med() static K Med(K kmin,K kmax) // kmin<kmax { return K( kmin+(kmax-kmin-1)/2 ); } // class PrepareIns class PrepareIns : NoCopy { .... public: T *found; PrepareIns(T **root_ptr,K key); PrepareIns(Root &root,K key); PrepareIns(T **root_ptr,K key,K kmin,K kmax); PrepareIns(Root &root,K key,K kmin,K kmax); void complete(T *node); }; // struct Check struct Check { K minval; K maxval; Check(T *root,K kmin,K kmax); .... }; };
RadixAlgo extends BinAlgo with a Radix Tree functionality. The K must be an unsigned integral type. Each Radix Tree has a value range. It may be the full value range of the given type K, or some shorter range. Anyway, you have to use the same range for all operations with a particular tree.
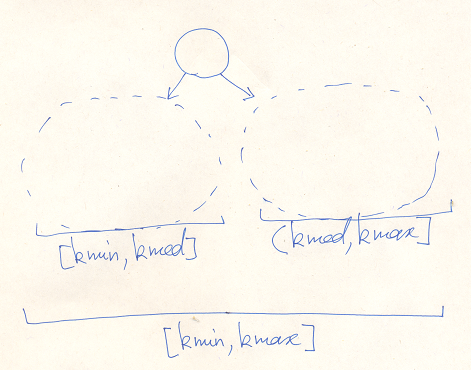
Med() is used to split a value range. If the tree value range is [kmin,kmax], and kmed == Med(kmin,kmax), then the Lo subtree has a value range [kmin,kmed] and the Hi subtree — [kmed+1,kmax].
PrepareIns is a tool to insert an element into the tree. Its constructor prepares the operation. Its arguments are: the root double pointer (or the reference to a Root object), the key, and, optionally, the value range. If the value range is omitted, then the full range is assumed. There are two cases. First, there exist an element with the given key already. In such case, the pointer to this element is returned in the member found. Otherwise, found is null and you may do insert using the method complete(). You must provide an element to be inserted. The key will be placed into the link of this element. If you do not complete the operation, the tree remains in the original logical state, but probably with some tree structure modifications.
Check performs the tree structure check. This type is for testing purpose mostly. Constructor takes the root pointer and the value range. If the tree is broken, an exception is thrown. Otherwise, minval and maxval members will be assigned with the minimum and maximum value of keys in the tree (or both 0 if the tree is empty).
The TreeUpLink is another tree link. It has the additional member up. It points to the parent element. For the root node it is null. Keys are not unique. In fact, this kind of tree is a combination of tree and list. There are two kind of links: normal tree links, and same-key links, where lo==this. And the Lo and Hi subtrees may have nodes with the same key as the root element.
template <class T,class K>
struct TreeUpLink
{
T *lo; // == this for same-key nodes
T *hi;
T *up;
K key; // non-unique
using Node = TreeUpLink<T,K> ;
template <TreeUpLink<T,K> T::* LinkMember,class KRef=K> struct BinAlgo;
template <TreeUpLink<T,K> T::* LinkMember> struct RadixAlgo;
};
BinAlgo is essentially the same as for the TreeLink.
struct BinAlgo
{
// node!=0
// root_ptr!=0
static Node & Link(T *node) { return node->*LinkMember; }
// Find
static T * Find(T *root,KRef key); // == key
static T * FindMin(T *root);
static T * FindMin(T *root,KRef key); // min >= key
static T * FindMax(T *root);
static T * FindMax(T *root,KRef key); // max <= key
The family of Find...() functions is the same.
// Del static T * DelRoot(T *root); // root!=0 static void Del(T **root_ptr,T *node); static T * Del(T **root_ptr,KRef key); static T * DelMin(T **root_ptr); static T * DelMin(T **root_ptr,KRef key); static T * DelMax(T **root_ptr); static T * DelMax(T **root_ptr,KRef key);
Again, the family of Del...() functions is the same.
// struct Root
struct Root
{
T *root;
// constructors
Root() { init(); }
// methods
void init() { root=0; }
T * operator + () const { return root; }
bool operator ! () const { return !root; }
// find
T * find(KRef key) const { return Find(root,key); }
T * findMin() const { return FindMin(root); }
T * findMin(KRef key) const { return FindMin(root,key); }
T * findMax() const { return FindMax(root); }
T * findMax(KRef key) const { return FindMax(root,key); }
// del
T * del(KRef key) { return Del(&root,key); }
T * delMin() { return DelMin(&root); }
T * delMin(KRef key) { return DelMin(&root,key); }
T * delMax() { return DelMax(&root); }
T * delMax(KRef key) { return DelMax(&root,key); }
void del(T *node) { Del(&root,node); }
// replace
void replace(T *place,T *obj); // place!=0 linked, obj!=0 unlinked
};
};
The Root is the same too, except, there is no locate() family of methods. There is also the additional method replace().
replace() replaces the given tree node with another unlinked node. The new node becomes a member of the tree, the old one becomes unlinked. Keys are swapped.
struct RadixAlgo : BinAlgo { // Med() static K Med(K kmin,K kmax) // kmin<kmax { return kmin+(kmax-kmin-1)/2; } // Ins static void Ins(BinAlgo::Root &root,T *node,K kmin,K kmax); static void Ins(T **root_ptr,T *node,K kmin,K kmax); static void Ins(BinAlgo::Root &root,T *node); static void Ins(T **root_ptr,T *node); // class PrepareIns class PrepareIns : NoCopy { .... public: T *found; PrepareIns(T **root_ptr,K key); PrepareIns(BinAlgo::Root &root,K key); PrepareIns(T **root_ptr,K key,K kmin,K kmax); PrepareIns(BinAlgo::Root &root,K key,K kmin,K kmax); void complete(T *node); }; // struct Root struct Root : BinAlgo::Root { void ins(T *node,K kmin,K kmax); void ins(T *node,K key,K kmin,K kmax); void ins(T *node); void ins(T *node,K key); }; // struct Check struct Check { K minval; K maxval; Check(T *root,K kmin,K kmax); .... }; };
RadixAlgo extends the BaseAlgo.
Med() is the same.
PrepareIns is the same.
Check is the same.
The main difference is insertion algorithms. You may choose between PrepareIns as for TreeLink. In this case you will have the same property tree with unique keys. Or you may choose the Ins() family of insertion functions. In this case keys are not unique and you may always insert an element into the tree. There are four of them. The first argument is the double root pointer or the BaseAlgo::Root reference. The second argument is the element to be inserted. The element must have the key inside initialized. Two last arguments, if any, specifies the tree value range.
The RadixAlgo Root extends the BaseAlgo Root with the insertion methods. Two of them are direct calls of the correspondent Ins() functions. Another two have the additional argument key. This key is placed into the element link before insertion.
RBTreeLink is a Red-Black Tree link. It has the additional member: RBFlag flag. This flag determines arrows colors:
enum RBFlag { RBFlag_BlackBlack, RBFlag_HiRed, RBFlag_LoRed, RBFlag_RedRed }; template <class T,class K> struct RBTreeLink { T *lo; T *hi; K key; // unique RBFlag flag; using Node = RBTreeLink<T,K> ; template <RBTreeLink<T,K> T::* LinkMember,class KRef=K> struct BaseAlgo; template <RBTreeLink<T,K> T::* LinkMember,class KRef=K> struct Algo; template <RBTreeLink<T,K> T::* LinkMember,class KRef=K> struct AltAlgo; };
There are tree Algorithm Packages for this link: BaseAlgo, Algo and AltAlgo. AltAlgo is an alternative implementation of the same operations, as Algo.
struct BaseAlgo { // node!=0 static Node & Link(T *node) { return node->*LinkMember; } // Find static T * Find(T *root,KRef key); // == key static T * FindMin(T *root); static T * FindMin(T *root,KRef key); // min >= key static T * FindMax(T *root); static T * FindMax(T *root,KRef key); // max <= key // struct Check struct Check { K minval; K maxval; int height; bool black_black; explicit Check(T *root); .... }; };
This package contains find operations and the Check. Find operations are exactly the same as find operations of the TreeLink. Check has the same meaning too. It just has different arguments: there are no range variables. And it returns additional information: height is a black height of the tree, black_black is true, if two root arrows of the tree are black.
struct Algo : BaseAlgo
{
// node!=0
// root_ptr!=0
// Del
static T * DelMin(T **root_ptr);
static T * DelMax(T **root_ptr);
static T * Del(T **root_ptr,KRef key);
static void Del(T **root_ptr,T *node);
Algo extends BaseAlgo with delete operations, insert operation and Root.
There are four delete functions with the same semantic as TreeLink delete functions.
// struct Root
struct Root
{
T *root;
// constructors
Root() { init(); }
// methods
void init() { root=0; }
T * operator + () const { return root; }
bool operator ! () const { return !root; }
// find
T * find(KRef key) const { return Find(root,key); }
T * findMin() const { return FindMin(root); }
T * findMin(KRef key) const { return FindMin(root,key); }
T * findMax() const { return FindMax(root); }
T * findMax(KRef key) const { return FindMax(root,key); }
// del
T * delMin() { return DelMin(&root); }
T * delMax() { return DelMax(&root); }
T * del(KRef key) { return Del(&root,key); }
void del(T *node) { Del(&root,node); }
};
Root encapsulates a root pointer and tree operations. The methods are direct calls of the correspondent functions.
// class PrepareIns
class PrepareIns : NoCopy
{
....
public:
T *found;
PrepareIns(T **root_ptr,KRef key);
PrepareIns(Root &root,KRef key);
void complete(T *node);
};
};
PrepareIns is a tool to insert an element into the tree. Its constructor prepares the operation. Its arguments are: the root double pointer (or the reference to a Root object) and the key. There are two cases. First, there exist an element with the given key already. In such case, the pointer to this element is returned in the member found. Otherwise, found is null and you may do insert using the method complete(). You must provide an element to be inserted. The key will be placed into the link of this element. If you do not complete the operation, the tree remains in the original logical state, but probably with some tree structure modifications.
RBTreeUpLink is another Red-Black Tree link. It contains the additional up pointer, this pointer points to the parent tree element. For the root element it is null.
template <class T,class K>
struct RBTreeUpLink
{
T *up;
T *lo;
T *hi;
K key; // unique
RBFlag flag;
using Node = RBTreeUpLink<T,K> ;
template <RBTreeUpLink<T,K> T::* LinkMember,class KRef=K> struct BaseAlgo;
template <RBTreeUpLink<T,K> T::* LinkMember,class KRef=K> struct Algo;
};
There are two Algorithm Packages for this link: BaseAlgo and Algo. They content are the same as for the RBTreeLink packages. The only difference, the struct Root has the additional method replace().
// replace
void replace(T *place,T *obj); // place!=0 linked, obj!=0 unlinked
};
replace() replaces the given tree node with another unlinked node. The new node becomes a member of the tree, the old one becomes unlinked. Keys are swapped.